
GRAVITY VERSUS THE GRAVITY PIT
In this experiment, we use an analogy of coins rolling around a pit to explain how planets move around the Sun.
According to Eistein’s general theory of relativity, the Sun’s mass warps space and time around it. Planets follow paths called geodesics through that warped spacetime. The warping of four-dimensional space is difficult to visualize, but we can gain some understanding of it by thinking about the coin pit, which is a two-dimensional surface warped into a third dimension. The geodesic paths followed by planets through warped four-dimensional spacetime form orbits around the Sun. Similarly, coins orbit the center of the warped gravity pit. Since spacetime near the Sun is warped more than spacetime further away, planets move faster near the Sun. Similarly, coins near the center of the gravity pit move faster.
Of course, there are some important differences to think about too. For example, why do coins spiral into the center of the pit in a matter of minutes while planets (fortunately) do not? We’ll leave you to think about that.
Before Einstein’s general theory of relativity, gravity was understood in terms of Newton’s law of universal gravitation. Although this proved inadequate to fully explain gravity, many aspects of planetary orbits are well described by this law. It is interesting to compare Newtonian gravity and the coin pit.
In the theory of Newtonian gravity, the planets are kept in their orbit by the force of gravity (FG) that the sun exerts on them. Newton’s law of gravitation specifies the force:
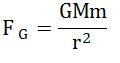
where G is the gravitational constant, M is the mass of the Sun, m is the mass of the planet and r is the distance between the planet and the Sun.
The force of gravity is strongest when the distance r between the Sun and the planet is smallest.
The centripetal force (FC) is 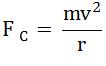 where v is the speed of the planet.
where v is the speed of the planet.
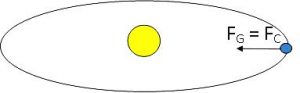
For simplicity, let’s assume the orbit of a planet is circular. Elliptical orbits that aren’t exactly circular will still have some similarities to the results we derive. For a circular orbit in this system FG = FC ; This equation can be solved for v:
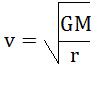
The important result is that v is proportional to 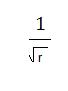
In conclusion
- The force of gravity is strongest near the Sun.
- The speed of a planet is greatest close to the Sun.
- That implies that the period of a planet is shortest for orbits closest to the Sun.
- The orbit does not depend on the mass of the planet.
The Physics of the Coin Pit
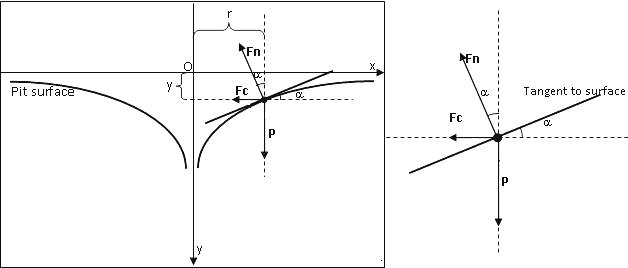
The downward force of gravity on the coin is P = mg, where m is the mass of the coin and g is the acceleration due to gravity. A normal force Fn pushes out on the coin from the surface of the pit. The vertical component of Fn must be equal in magnitude to P, so Fn cos(α) = P = mg.
Assuming the coin follows a circular orbit with radius r around the center of the pit, the horizontal component of Fn provides the centripital force: Fn sin(α) = Fc = mv2/r.
By dividing the above equations by each other, we get tan(α) = sin(α)/cos(α) = v2/(gr).
The pit is designed so that tan(α) = k/r2.
The above two equations for tan(α) can be combined to solve for v, yielding 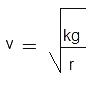
As with the solar system, v in the coin pit is proportional to 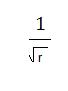
In conclusion
- The slope of the gravity pit is greatest near the center.
- The speed of the coin is greatest when the coin is near the center.
- This implies that the period of revolution of the coin is shortest when the coin is closer to the center of the pit.
- The orbit of the coin does not depend on its mass. (Does this prediction from the theory agree with your observations?)