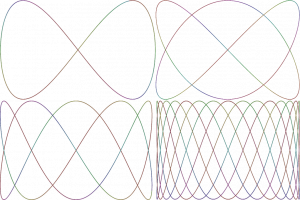
[Lissajous Curve Plotter] ← Try it on your own device!
Two oscillations are used to produce a graph called a Lissajous curve (pronounced Liss-uh-joo). One oscillation determins the x coordinate and the other oscillation determines the y coordinate. In this demonstration, a third oscillation determines the drawing color.
When the ratio of the frequencies of the oscillations is a rational number (i.e. expressible as integers a/b), the curve is closed; it loops back on itself. Different ratios produce different shapes.
Musical Scales
Sound is an oscillation. In this demonstration of Lissajous curves, musical tones are used as the oscillations that produce the curve.
The various tones of a musical scale are not selected at random. It was found by many different cultures that if two tones were played together, the combination would sound pleasant (consonant) in some cases. An important source of consonance is when the ratio of the frequencies (the interval) is expressible as a fraction of low integers a/b.
The various tones in a scale are traditionally given letters and names; the ratio of their frequencies to the base tone is given below for the major C just scale.
| DO | RE | MI | FA | SOL | LA | TI | DO’ |
|---|---|---|---|---|---|---|---|
| C | D | E | F | G | A | B | C’ |
| 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 |
The just scale is designed to produce intervals that form perfect ratios with the base tone in the scale. Other musical scales are designed with different considerations in mind. A commonly used system known as the equal tempered scale does not have perfect ratios with the base tone, but it has the advantage that any tone in the scale can be chosen as the base tone while maintaining the same intervals in the scale and the same set of frequencies to choose from. In the just scale, on the other hand, the set of frequencies must be adjusted, depending on which base tone was chosen. Since many of the intervals in the equal tempered scale are close but not quite perfect ratios, the Lissajous curve does not quite loop back on itself as it does when using frequencies from the just scale.
The ratio of frequencies to the base tone for the major C equal tempered scale are given below.
| DO | RE | MI | FA | SOL | LA | TI | DO’ |
|---|---|---|---|---|---|---|---|
| C | D | E | F | G | A | B | C’ |
| 1 | 22⁄12 | 24⁄12 | 25⁄12 | 27⁄12 | 29⁄12 | 211⁄12 | 2 |