Welcome, Professor Ben Woods!

Posted on October 17, 2024

Ben Woods

Condensed matter theorist Ben Woods joined the department as an assistant professor this fall. Originally from a small town in North Dakota, Woods studied physics at the University of North Dakota and earned a PhD in physics from West Virginia University. He first came to UW–Madison for a postdoc with Mark Friesen in 2021, and now moves into his faculty role.

Please give an overview of your research.

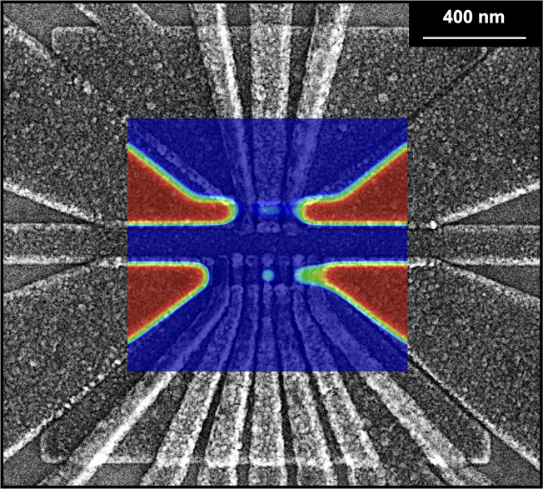
I primarily work in two main areas of condensed matter theory and quantum information science. The first area is the theory of semiconductor quantum dots, with applications towards building and operating quantum computers based on spin qubits. Quantum dots can be thought of as artificial atoms in which electrons are trapped and manipulated within a semiconductor, such as silicon, by metallic gates that sit on top of the semiconductor. An electron in the quantum dot forms the basis for a type of qubit called a spin qubit, where the quantum information is stored in the spin of the electron. I investigate how we can build higher quality spin qubits. One aspect of this is analyzing and designing single and two qubit gates such that their efficiency and noise resiliency can be improved. Another aspect is studying the materials and design of quantum dot devices to optimize certain properties, such as how the qubits respond to an external magnetic field. I am also interested in quantum dot arrays as a platform for quantum simulation. Here the idea is to engineer the interactions between the quantum dots to emulate a quantum system of interest.

The other area I work in is semiconductor-superconductor heterostructures. Here, you’re trying to combine desirable properties of both types of materials to create interesting devices that would otherwise be impossible. I study semiconductor-superconductor heterostructures that can give rise to exotic particles known as Majorana zero modes, which form the basis for topological qubits. These qubits are immune to certain error sources that more conventional types of qubits are not. I am trying to understand the effects of disorder on these heterostructures and develop new schemes in which Majorana zero modes can be realized.

What are one or two of the main projects your group will work on first?

One initial project will focus on designing a new qubit architecture for quantum dot spin qubits. In the most conventional type of spin qubit, you have a single electron spin that is manipulated by jiggling it with an electric field back and forth within a single quantum dot. It turns out, however, that these qubits can be manipulated more efficiently if you can hop electrons between multiple quantum dots. Specifically, I’ve devised new schemes involving three dots in a triangular geometry in which single-qubit gates can be performed quite efficiently. These ideas work in principle, but now it’s a matter of quantitatively studying how noise resilient the scheme is and how finely tuned the system parameters need to be for things to go as planned.

A second initial project is more towards quantum simulation using quantum dot arrays. The project will focus on studying magnetism in quantum dot arrays. In other words, asking how the spins of the quantum dot electrons organize due to their mutual interaction. One interesting wrinkle in these quantum dot arrays based on silicon is that there is a valley degree of freedom in addition to the usual spin degree of freedom. The project involves understanding the effects on the magnetic ordering due to this additional valley degree of freedom. Specifically, I am interested in how fluctuations in the valley degree of freedom from one dot to the next can impact magnetic ordering.

What attracted you to Madison and the university?

There were two main reasons. First, my wife had gotten a residency as an anesthesiologist at the UW hospital. So that was an obvious motivation. Second, one of my grad school advisors knew Mark Eriksson and Mark Friesen and thought it’d be a natural fit for me to work with them as a postdoc. Since moving here, my family has enjoyed Madison, and I really like the physics department. The people are very friendly and collaborative. I am incredibly happy to be able to stay in Madison and at the UW physics department.

What is your favorite element and/ or elementary particle?

It has to be silicon, right? It’s the material I think about every day. And the world economy is largely based on stuff made with silicon. So that’s pretty cool?

What hobbies and interests do you have?

I like to play guitar, read, watch sports, and spend time with my family and friends. I have two kids, three years and six months old, who I like to spend most of my free time on.

Welcome, assistant professor Ilya Esterlis

Posted on December 27, 2022

Ilya Esterlis

When Lake Mendota freezes over in the winter and thaws in the spring, those water/ice phase transitions might seem mundane. But, says new assistant professor of physics Ilya Esterlis, interesting things happen during phase transitions, and commonalities exist between phase transitions of any matter.

“That’s very surprising and strange sounding, but it turns out that there’s a very general framework in which to understand [these commonalities],” Esterlis says. “It’s this notion of universality, and by studying phase transitions you’re simultaneously studying a very broad class of materials.”

Esterlis, a condensed matter theorist whose research focuses on materials and phase transitions, joins the department January 1, 2023. He is currently a postdoctoral fellow at Harvard, and joined us for a virtual interview earlier this fall.

Can you please give an overview of your research?

I am a condensed matter theorist, so I study materials, and in particular I try to classify different phases of matter and the phase transitions between those phases of matter. I’m mostly interested in electronic systems, where you have a large macroscopic number of interacting electrons and are trying to understand the kind of phenomena that can emerge when you have that large number of degrees of freedom interacting with one another. And a lot of these things are motivated by experiments — not all of them. There are some more academic questions that I’m interested in investigating and they’re a bit more formal. But I’m also motivated by interesting things that are happening in the lab. Part of my work is not only trying to characterize and understand phases of matter, but also trying to propose ways that different phases could be detected experimentally, how they would manifest themselves in different experimental signatures.

I’m also interested in superconductivity. My PhD work focused a lot on trying to understand the optimal conditions for making superconductors — if you could have every knob at your disposal, what would you do to optimize them? Optimize in this case means: make superconductors that exist at as high of a temperature as possible. Superconductivity is typically a low temperature phenomenon, so there’s a holy grail in condensed matter physics trying to make higher temperature superconductors. Part of my work has been organized around trying to understand what would be even in principle the optimal route towards achieving higher temperature superconductors.

Once you’re in Madison, what are one or two research projects you and your group will focus on?

I will focus a good amount of my research efforts on studying superconductivity, continuing this line of investigation into what the optimal conditions for superconductors are. If you had all the freedom in the world, how would you build the best superconductor that exists to high temperatures and under normal laboratory conditions? Not under extreme, unrealistic conditions but in an everyday parameter regime. And that involves understanding the superconducting state itself. Superconductors are a phase of matter that is distinct from, say, a metal, which is also a good conductor but not a superconductor. But oftentimes to understand superconductors better, one has to understand the state from which they came. That is to say, you take a metal and you cool it down to low temperatures and it goes from being a good conductor to a superconductor. To understand that superconductor, it’s often helpful to understand the metal from which it came at higher temperature. And sometimes those metals can be conventional, like copper wires, but sometimes they can be very unconventional metals and strange for various reasons. One open question is: what is the interplay between superconductivity and unusual metals? If you take a high temperature unusual metal, what is the kind of superconductor that it turns into at lower temperature? And unusual in this context means that it has some properties that are not typical to conventional metals. For instance, there’s predictions for how resistance changes with temperature in a conventional metal but unusual metals have rather different resistance behaviors.

What is your favorite element and/or elementary particle?

Helium is remarkable in that it has a number of unusual properties. For instance, if you cool it down to zero temperature it does not crystallize, it remains a liquid. That’s solely due to quantum mechanics, which is kind of an incredible thing. If you do make it crystallize by applying pressure, then that solid itself also has very interesting properties.

And my favorite elementary particle is the anyon. It’s not elementary, say, in the sense of electrons or quarks. But it’s this really remarkable thing that happens in condensed matter systems where if you take a macroscopic number of electrons and you subject them to a very large magnetic field, then a remarkable thing happens where the behavior of the system, as viewed kind of on macroscopic scales, does not look like the behavior of electrons, it really looks like the behavior of particles called anyons that have fractional electric charge. So they are elementary in condensed matter physics.

What hobbies and interests do you have?

I really love to play music, guitar specifically. And I have two small kids, two daughters, and I just like hanging out with them.

Cross-institutional collaboration leads to new control over quantum dot qubits

Posted on August 31, 2022

a greyscale image makes up the border of this square image, with a full-color square in the exact center. the image shows tiny tunnel-like features, all congregating in the middle

This story was originally published by the Chicago Quantum Exchange

Qubits are the building blocks of quantum computers, which have the potential to revolutionize many fields of research by solving problems that classical computers can’t.

But creating qubits that have the perfect quality necessary for quantum computing can be challenging.

Researchers at the University of Wisconsin–Madison, HRL Laboratories LLC, and University of New South Wales (UNSW) collaborated on a project to better control silicon quantum dot qubits, allowing for higher-quality fabrication and use in wider applications.

All three institutions are affiliated with the Chicago Quantum Exchange. The work was published in Physical Review Letters, and the lead author, J. P. Dodson, has recently transitioned from UW–Madison to HRL.

“Consistency is the thing we’re after here,” says Mark Friesen, Distinguished Scientist of Physics at UW–Madison and author on the paper. “Our claim is that there is actually hope to create a very uniform array of dots that can be used as qubits.”

Sensitive quantum states

While classical computer bits use electric circuits to represent two possible values (0 and 1), qubits use two quantum states to represent 0 and 1, which allows them to take advantage of quantum phenomena like superposition to do powerful calculations.

Qubits can be constructed in different ways. One way to build a qubit is by fabricating a quantum dot, or a very, very small cage for electrons, formed within a silicon crystal. Unlike qubits made of single atoms, which are all naturally identical, quantum dot qubits are man-made—allowing researchers to customize them to different applications.

But one common wrench in the metaphorical gears of these silicon qubits is competition between different kinds of quantum states. Most qubits use “spin states” to represent 0 and 1, which rely on a uniquely quantum property called spin. But if the qubit has other kinds of quantum states with similar energies, those other states can interfere, making it difficult for scientists to effectively use the qubit.

In silicon quantum dots, the states that most often compete with the ones needed for computing are “valley states,” named for their locations on an energy graph—they exist in the “valleys” of the graph.

To have the most effective quantum dot qubit, the valley states of the dot must be controlled such that they do not interfere with the quantum information-carrying spin states. But the valley states are extremely sensitive; the quantum dots sit on a flat surface, and if there is even one extra atom on the surface underneath the quantum dot, the energies of the valley states change.

The study’s authors say these kinds of single-atom defects are pretty much “unavoidable,” so they found a way to control the valley states even in the presence of defects. By manipulating the voltage across the dot, the researchers found they could physically move the dot around the surface it sits on.

“The gate voltages allow you to move the dot across the interface it sits on by a few nanometers, and by doing that, you change its position relative to atomic-scale features,” says Mark Eriksson, John Bardeen Professor and chair of the UW–Madison physics department, who worked on the project. “That changes the energies of valley states in a controllable way.

“The take home message of this paper,” he says, “is that the energies of the valley states are not determined forever once you make a quantum dot. We can tune them, and that allows us to make better qubits that are going to make for better quantum computers.”

Building on academic and industry expertise

The host materials for the quantum dots are “grown” with precise layer composition. The process is extremely technical, and Friesen notes that Lisa Edge at HRL Laboratories is a world expert.

“It requires many decades of knowledge to be able to grow these devices properly,” says Friesen. “We have several years of collaborating with HRL, and they’re very good at making really high-quality materials available to us.”

The work also benefitted from the knowledge of Susan Coppersmith, a theorist previously at UW–Madison who moved to UNSW in 2018. Eriksson says the collaborative nature of the research was crucial to its success.

“This work, which gives us a lot of new knowledge about how to precisely control these qubits, could not have been done without our partners at HRL and UNSW,” says Eriksson. “There’s a strong sense of community in quantum science and technology, and that is really pushing the field forward.”

Opening doors to quantum research experiences with the Open Quantum Initiative

Posted on August 29, 2022

This past winter, Katie Harrison, then a junior physics major at UW–Madison, started thinking about which areas of physics she was interested in studying more in-depth.

“Physics is in general so broad, saying you want to research physics doesn’t really cut it,” Harrison says.

She thought about which classes she enjoyed the most and talked to other students and professors to help figure out what she might focus on. Quantum mechanics was high on her list. During her search for additional learning opportunities, she saw the email about the Open Quantum Initiative (OQI), a new fellowship program run by the Chicago Quantum Exchange (CQE).

“This could be something I’m interested in, right?” Harrison thought. “I’ll apply and see what happens.”

What happened was that Harrison was one of 12 undergraduate students accepted into the inaugural class of OQI Fellows. These students were paired with mentors at CQE member institutions, where they conducted research in quantum science information and engineering. OQI has a goal of connecting students with leaders in academia and industry and increasing their awareness of quantum career opportunities. The ten-week Fellowship ran through August 19.

11 students pose on a rock wall, all students are wearing the same Chicago Quantum Exchange hooded sweatshirt — OQI students attend a wrap-up at the University of Chicago on August 17. Each student presented at a research symposium that day, which also included a career panel from leaders across academia, government, and industry and an opportunity to network. | Photo provided by the Chicago Quantum Exchange

OQI also places an emphasis on establishing diversity, equity, and inclusion as priorities central to the development of the quantum ecosystem. Almost 70% of this year’s fellowship students are Hispanic, Latino, or Black, and half are the first in their family to go to college. In addition, while the field of quantum science and engineering is generally majority-male, the 2022 cohort is half female.

This summer, UW–Madison and the Wisconsin Quantum Institute hosted two students: Harrison with physics professor Baha Balantekin and postdoc Pooja Siwach; and MIT physics and electrical engineering major Kate Arutyunova with engineering physics professor Jennifer Choy, postdoc Maryam Zahedian and graduate student Ricardo Vidrio.

Harrison and Arutyunova met at OQI orientation at IBM’s quantum research lab in New York, and they hit it off immediately. (“We have the most matching energies (of the fellows),” Arutyunova says, with Harrison adding, “The synergy is real.”)

Four people stand in a lab in front of electronics equipment — OQI Fellow Kate Arutyunova with her research mentors. (L-R) Engineering Physics professor Jennifer Choy, graduate student Ricardo Vidrio, Kate Arutyunova, and postdoc Maryam Zahedian. | Photo provided by Kate Arutyunova

Despite their very different research projects — Harrison’s was theoretical and strongly focused on physics, whereas Arutyunova’s was experimental and with an engineering focus — they leaned on each other throughout the summer in Madison. They met at Union South nearly every morning at 7am to read and bounce ideas off each other. Then, after a full day with their respective research groups, they’d head back to Union South until it closed.

Modeling neutrino oscillations

Harrison’s research with Balantekin and Siwach investigated the neutrinos that escape collapsing supernovae cores. Neutrinos have a neutral charge and are relatively small particles, they make it out of cores without interacting with much — and therefore without changing much — so studying them helps physicists understand what is happening inside those stars. However, this is a difficult task because neutrinos oscillate between flavors, or different energy levels, and therefore require a lot of time and resources to calculate on a classical computer.

Harrison’s project, then, was to investigate two types of quantum computing methods, pulse vs circuit based, and determine if one might better fit their problem than the other. Previous studies suggest that pulsed based is likely to be better, but circuit based involves less complicated input calculations.

“I’ve been doing calibrations and calculating the frequencies of the pulses we’ll need to send to our qubits in order to get data that’s as accurate as a classical computer,” Harrison says. “I’m working with the circuit space, the mathematical versions of them, and then I’ll send my work to IBM’s quantum computers and they’ll calculate it and give results back.”

While she didn’t fully complete the project, she did make significant progress.

“(Katie) is very enthusiastic and she has gone a lot further than one would have expected an average undergraduate could have,” Balantekin says. “She started an interesting project, she started getting interesting results. But we are nowhere near the completion of the project, so she will continue working with us next academic year, and hopefully we’ll get interesting results.”

Developing better quantum sensors

Over on the engineering side of campus, Arutyunova was studying different ways to introduce nitrogen vacancy (NV) centers in diamonds. These atomic-scale defects are useful in quantum sensing and have applications in magnetometry. Previous work in Choy’s group made the NV centers by a method known as nitrogen ion beam implantation. Arutyunova’s project was to compare how a different method, electron beam irradiation, formed the NV centers under different starting nitrogen concentrations in diamond.

Briefly, she would mark an edge of a very tiny (2 x 2 x 0.5 millimeter), nitrogen-containing diamond, and irradiate the sample with a scanning electron microscope. She used confocal microscopy to record the initial distribution of NV centers, then moved the sample to the annealing step, where the diamond is heated up to 1200 celsius in a vacuum annealing furnace. The diamonds are then acid washed and reexamined with the confocal microscope to see if additional NV centers are formed.

“It’s a challenging process as it requires precise coordinate-by-coordinate calculation for exposed areas and extensive knowledge of how to use the scanning electron microscope,” says Arutyunova, who will go back to MIT after the fellowship wraps. “I think I laid down a good foundation for future steps so that the work can be continued in my group.”

Choy adds:

Kate made significant strides in her project and her work has put us on a great path for our continued investigation into effective ways of generating color centers in diamond. In addition to her research contributions, our group has really enjoyed and benefited from her enthusiasm and collaborative spirit. It’s wonderful to see the relationships that Kate has forged with the rest of the group and in particular her mentors, Maryam and Ricardo. We look forward to keeping in touch with Kate on matters related to the project as well as her academic journey.

Beyond the summer fellowship

Both Harrison and Arutyunova think that this experience has drawn them to the graduate school track, likely with a focus on quantum science. More importantly, it has helped them both to learn what they like about research.

“I would prefer to work on a problem and see the final output rather than a question where I do not have an idea of the application,” Arutyunova says. “And I realized how much I like to collaborate with people, exchange ideas, propose something, and listen to people and what they think about research.”

They also offer similar advice to other undergraduate students who are interested in research: do it, and start early.

“No matter when you start, you’re going to start knowing nothing,” Harrison says. “And if you start sooner, even though it’s scary and you feel like you know even less, you have more time to learn, which is amazing. And get in a research group where they really want you to learn.”

Undergraduate quantum science research fellowship launches

Posted on October 28, 2021

This story was originally published by the Chicago Quantum Exchange

The Open Quantum Initiative (OQI), a working group of students, researchers, educators, and leaders across the Chicago Quantum Exchange (CQE), announced the launch of the OQI Undergraduate Fellowship as part of their effort to advocate for and contribute to the development of a diverse and inclusive quantum workforce.

The primary mission of the OQI is to champion the development of a more inclusive quantum community. Science, technology, engineering, and mathematics (STEM) fields remain overwhelmingly white and male—only about 20% of bachelor’s degrees in physics, engineering, and computer science go to women, a mere 6% of all STEM bachelor’s degrees are awarded to African American students, and 12% of all STEM bachelor’s degrees are awarded to Hispanic students. But as the field of quantum science is still relatively new compared to other STEM subjects, groups like the OQI see a chance to make the foundations of the field diverse and accessible to all from the start.

“In many respects, we are building a national workforce from the ground up,” says David Awschalom, the Liew Family Professor in Molecular Engineering and Physics at the University of Chicago, senior scientist at Argonne National Laboratory, director of the Chicago Quantum Exchange, and director of Q-NEXT, a Department of Energy quantum information science center led by Argonne. “There are incredible opportunities here to make the field of quantum engineering as inclusive and equitable as possible from the very beginning, creating a strong ecosystem for the future.”

At the heart of the OQI’s effort is a new fellowship starting in summer 2022. For 10 weeks, fellows will live and work at a CQE member or partner institution, completing a research project in quantum information science and engineering under the guidance of a mentor. Students will have numerous opportunities to interact with the other fellows in their cohort during the summer research period and throughout the following academic year.

Through this fellowship, the students can expand their understanding of quantum science, receive career guidance, and grow their professional networks with leaders in academia and industry. The OQI will also aim to provide future research experiences in subsequent summers, as well as provide opportunities to mentor future fellows, helping to build a larger, diverse quantum community over time.

With the support of CQE’s member and partner institutions, including the University of Chicago, Argonne, Fermilab, University of Illinois Urbana-Champaign, University of Wisconsin-Madison, Northwestern University, and The Ohio State University, along with the NSF Quantum Leap Challenge Institute for Hybrid Quantum Architectures and Networks (HQAN) and Q-NEXT, this fellowship helps to establish diversity, equity, and inclusion as priorities central to the development of the quantum ecosystem.

The OQI launched the fellowship alongside a workshop on September 22 and 23. The OQI workshop, titled “Building a Diverse Quantum Ecosystem,” brought together CQE students, researchers, and professionals from across different institutions, including industry, to discuss the prevailing issues and barriers in quantum information science as the field develops. Institutional changemakers also shared what they have learned from their own efforts to increase representation. A panel on education and workforce development at the upcoming Chicago Quantum Summit on Nov. 4 will continue the discussion on building inclusive onramps for the quantum information science field.

“For quantum science and engineering to achieve its full potential, it must be accessible to all,” says Kayla Lee, Academic Alliance Lead at IBM Quantum and keynote speaker of the OQI workshop. “The OQI Undergraduate Fellowship provides explicit support for historically marginalized communities, which is crucial to increasing quantum engagement in a way that creates a more diverse and equitable field.”

Applications for the OQI Undergraduate Fellowship are open now.

Researchers awarded Department of Energy Quantum Information Science Grant

Posted on December 7, 2020

Three UW–Madison physics professors and their colleagues have been awarded a U.S. Department of Energy (DOE) High Energy Physics Quantum Information Science award for an interdisciplinary collaboration between theoretical and experimental physicists and experts on quantum algorithms.

The grant, entitled “Detection of dark matter and neutrinos enhanced through quantum information,” will bring a total of $2.3 million directly to UW-Madison. Physics faculty include principal investigator Baha Balantekin as well as Mark Saffman, and Sue Coppersmith. Collaborators on the grant include Kim Palladino at the University of Oxford, Peter Love at Tufts University, and Calvin Johnson at San Diego State University.

With the funding, the researchers plan to use a quantum simulator to calculate the detector response to dark matter particles and neutrinos. The simulator to be used is an array of 121 neutral atom qubits currently being developed by Saffman’s group. Much of the research plan is to understand and mitigate the behavior of the neutral atom array so that high accuracy and precision calculations can be performed. The primary goal of this project is to apply lessons from the quantum information theory in high energy physics, while a secondary goal is to contribute to the development of quantum information theory itself.

New study expands types of physics, engineering problems that can be solved by quantum computers

Posted on August 25, 2020

A well-known quantum algorithm that is useful in studying and solving problems in quantum physics can be applied to problems in classical physics, according to a new study in the journal Physical Review A from University of Wisconsin–Madison assistant professor of physics Jeff Parker.

Quantum algorithms – a set of calculations that are run on a quantum computer as opposed to a classical computer – used for solving problems in physics have mainly focused on questions in quantum physics. The new applications include a range of problems common to physics and engineering, and expands on the types of questions that can be asked in those fields.

Jeff Parker

“The reason we like quantum computers is that we think there are quantum algorithms that can solve certain kinds of problems very efficiently in ways that classical computers cannot,” Parker says. “This paper presents a new idea for a type of problem that has not been addressed directly in the literature before, but it can be solved efficiently using these same quantum computer types of algorithms.”

The type of problem Parker was investigating is known as generalized eigenvalue problems, which broadly describe trying to find the fundamental frequencies or modes of a system. Solving them is crucial to understanding common physics and engineering questions, such as the stability of a bridge’s design or, more in line with Parker’s research interests, the stability and efficiency of nuclear fusion reactors.

As the system being studied becomes more and more complex — more components moving throughout three-dimensional space — so does the numerical matrix that describes the problem. A simple eigenvalue problem can be solved with a pencil and paper, but researchers have developed computer algorithms to tackle increasingly complex ones. With the supercomputers available today, more and more difficult physics problems are finding solutions.

“If you want to solve a three-dimensional problem, it can be very complex, with a very complicated geometry,” Parker says. “You can do a lot on today’s supercomputers, but there tends to be a limit. Quantum algorithms may be able to break that limit.”

The specific quantum algorithm that Parker studied in this paper, known as quantum phase estimation, had been previously applied to so-called standard eigenvalue problems. However, no one had shown that they could be applied to the generalized eigenvalue problems that are also common in physics. Generalized eigenvalue problems introduce a second matrix that ups the mathematical complexity.

Parker took the quantum algorithm and extended it to generalized eigenvalue problems. He then looked to see what types of matrices could be used in this problem. If the matrix is sparse — meaning, if most of the numerical components that make it up are zero — it means this problem could be solved efficiently on a quantum computer.

The study shows that quantum algorithms could be applied to classical physics problems, such as nuclear fusion mirror machines. | Credit: Cary Forest

“What I showed is that there are certain types of generalized eigenvalue problems that do lead to a sparse matrix and therefore could be efficiently solved on a quantum computer,” Parker says. “This type includes the very natural problems that often occur in physics and engineering, so this study provides motivation for applying these quantum algorithms more to generalized eigenvalue problems, because it hasn’t been a big focus so far.”

Parker emphasizes that quantum computers are in their infancy, and these classical physics problems are still best approached through classical computer algorithms.

“This study provides a step in showing that the application of a quantum algorithm to classical physics problems can be useful in the future, and the main advance here is it shows very clearly another type of problem to which quantum algorithms can be applied,” Parker says.

The study was completed in collaboration with Ilon Joseph at Lawrence Livermore National Laboratory. Funding support was provided by the U.S. Department of Energy to Lawrence Livermore National Laboratory under Contract No. DE-AC52-07NA27344 and U.S. DOE Office of Fusion Energy Sciences “Quantum Leap for Fusion Energy Sciences” (FWP SCW1680).