Like the classical computers we use every day, quantum computers can make mistakes when manipulating and storing the quantum bits (qubits) used to perform quantum algorithms. Theoretically, a quantum error correction protocol can correct these errors in a similar manner to classical error correction. However, quantum error correction is more demanding than its classical counterpart and has yet to be fully demonstrated, putting a limit on the functionality of quantum computers.
In a theory paper published in Nature Communications, UW–Madison physicist Shimon Kolkowitz and colleagues show a new way that quantum errors could be identified in one type of qubit known as neutral atoms. By pinpointing which qubit experienced an error, the study suggests that the requirements on quantum error correction can be significantly relaxed, approaching a level that neutral atom quantum computers have already achieved.

The study is a collaboration between two National Science Foundation Quantum Leap Challenge Institutes, Hybrid Quantum Architectures and Networks (HQAN) and Robust Quantum Simulation (RQS). UW–Madison is a member of HQAN.
“In quantum computing, a lot of the overhead in an error-correcting code is figuring out which qubit had the error. If I know which qubit it is, then the amount of redundancy needed for the code is reduced,” Kolkowitz says. “Neutral atom qubits are right on the edge of what you would call this fault-tolerant threshold, but no one has been able to fully realize it yet.”
Neutral atom qubits are made up of single atoms trapped with light. The logical gates between the atoms are performed by exciting the atoms to “Rydberg” states where the atom’s electron is excited far beyond its normal location. This quantum computing technique was first pioneered and experimentally demonstrated at UW–Madison by physics professors Mark Saffman and Thad Walker.
Currently, one error-corrected “logical” qubit is expected to require around 1000 physical qubits, exceeding the maximum number of qubits anyone has managed to wire together in any quantum computing system. Researchers have been studying different elements in Rydberg form as qubits for decades, gradually increasing their performance but not yet reaching the level required for error correction.
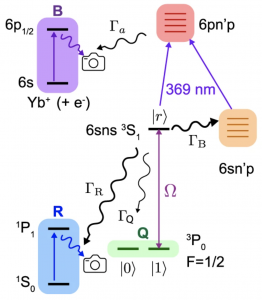
Knowing that eliminating qubit errors is not practical, Kolkowitz and colleagues instead asked if there might be a way to convert the errors into a type known as erasure errors. Named for the fact that the qubit has effectively vanished, or been erased, erasure errors can be beneficial because it is much easier to tell if a qubit is missing than if it is in the correct state or not.
They investigated the largely unstudied (in this context) element ytterbium because it has a relatively simple outer electron structure and its nucleus can only exist in two quantum spin states, +1/2 and -1/2. When manipulated into a metastable electronic state — a temporary state different than the true ground state — the qubit states are then set by the nuclear +1/2 and -1/2 spin states, and the quantum gates involve coupling one of these two qubit states to the Rydberg state.
“We knew that if an atom falls out of the metastable electronic state to the true ground state, we can detect that with a laser and still not screw up any of the other qubits at all,” Kolkowitz says. “But what that means is if I can set up a situation where errors manifest themselves as falling down into the ground state, I can just shine this laser and constantly check for errors and identify the qubit it happened in.”
In their first calculations using this metastable ytterbium platform, they showed that though errors still occur in the qubits as expected, around 98% of them would be converted to the detectable erasure errors.
But is that 98% error conversion rate good enough for a quantum computer in practice? The answer depends on the error threshold, a value that differs depending on the gates and qubits being used. The researchers next ran simulations of different numbers of quantum gates with a 98% erasure error conversion rate, or no conversion to erasure errors at all (as is currently standard).
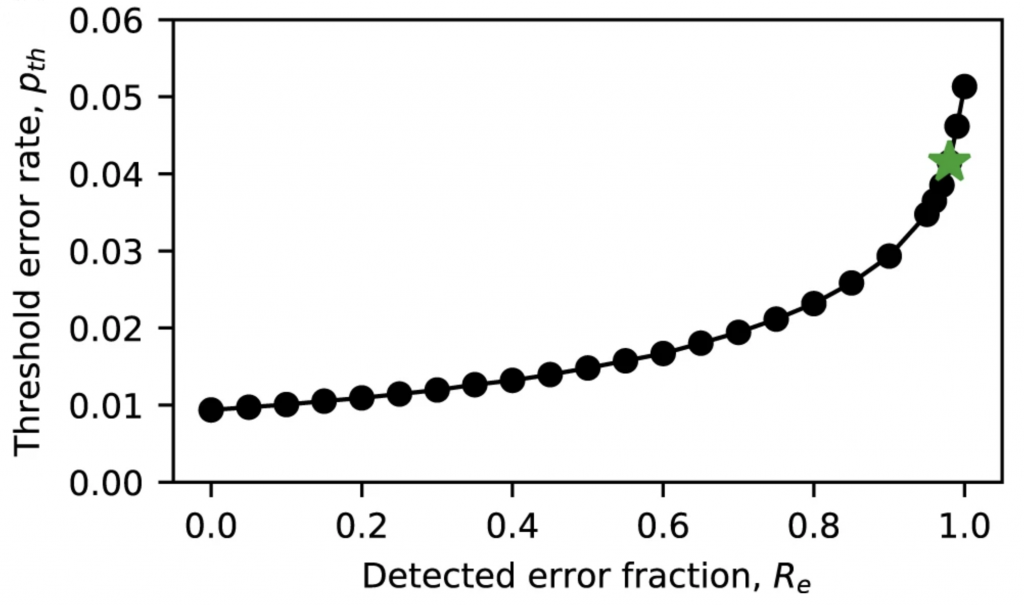
Without erasure error conversion, the error threshold is just shy of 1%, meaning each quantum gate would have to operate at over a 99% success probability to be fault tolerant. With erasure error conversion, however, the error threshold increases 4.4-fold, to just over 4%. And, for example, Saffman’s group has already demonstrated better than 4% error rates in neutral atom qubits.
The higher error threshold also means that there can be a higher ratio of logical qubits to physics qubits. Instead of one logical qubit per 1000 physical qubits, there could be around ten.
“And that’s the point of this work,” Kolkowitz says. “We show that if you can do this erasure conversion, it relaxes the requirements on both the error rates and on the number of atoms that you need.”
Co-author Jeff Thompson, an RQS investigator at Princeton, is already working to demonstrate these results experimentally in his lab. While other elements have been used in neutral atom quantum computing experiments before, until recently ytterbium was largely an unknown. Thompson’s group did much of the preliminary work to characterize the element and show that it could work well as the building block for a quantum computer.
“There were many open questions about ytterbium, and I’d say a lot of people who were using other elements are now moving into ytterbium based on Jeff’s groundwork,” Kolkowitz says. “And I expect that this study will accelerate that trend.”
Yue Wu and Shruti Puri at Yale University collaborated on this study. This work was supported by the National Science Foundation QLCI grants OMA-2120757 and OMA-2016136. Kolkowitz’s part of the work was additionally supported by ARO W911NF-21-1-0012.